Για την υλοποίηση του αλγορίθμου chain code χρησιμοποιείται ένα σύνολο συναρτήσεων, οι οποίες είναι υλοποιημένες σε διαφορετικά αρχεία. Πιο συγκεκριμένα, ο κώδικας που χρησιμοποιείται για την υλοποίηση του αλγορίθμου chain code είναι ο εξής:

Αρχείο chaincode

clear;

close all;

rgb = imread(‘homework5.bmp’);

imshow(rgb);

%convert RGB values to hue-saturation-value (HSV) color space.

%find out the flame on picture.

%when the brightness of pixel is over 0.999, I define it was the flame.

hsv = rgb2hsv(rgb);

i= hsv(:,:,3);

light=i>0.999;

%remove the redundant parts.

s = ones(3,3);

s1= ones(3,1);

light = imdilate(light,s1,1);

light = imerode(light,s1,1);

a = bwlabel(light);

b = a==1;

b = imdilate(b,s,2);

b = imerode(b,s,1);

b=double(b);

%figure,imshow(i);

figure,imshow(b);

%find out the edge of the flame

edg = edge(b,’canny’);

figure,imshow(edg);

hold on;

%defind the start point

[r c] = find(edg==1);

posit =[r c];

posit= sortrows(posit);

[m n]=size(posit);

plot(posit(1,2),posit(1,1),’-.r*’);

s= posit(1,1);t= posit(1,2);

posit(1,:)=[];

chain=[];

%find out the chain code.

for k =1: m-1

[o p]=size(posit);

for l=1:o

if posit(l,:)==[s t+1] %0

s= posit(l,1);t= posit(l,2);

posit(l,:)=[];

chain= [ chain 0];

break;

elseif posit(l,:)==[s-1 t+1] %1

s= posit(l,1);t= posit(l,2);

posit(l,:)=[];

chain= [ chain 1];

break;

elseif posit(l,:)==[s-1 t] %2

s= posit(l,1);t= posit(l,2);

posit(l,:)=[];

chain= [ chain 2];

break;

elseif posit(l,:)==[s-1 t-1] %3

s= posit(l,1);t= posit(l,2);

posit(l,:)=[];

chain= [ chain 3];

break;

elseif posit(l,:)==[s t-1] %4

s= posit(l,1);t= posit(l,2);

posit(l,:)=[];

chain= [ chain 4];

break;

elseif posit(l,:)==[s+1 t-1] %5

s= posit(l,1);t= posit(l,2);

posit(l,:)=[];

chain= [ chain 5];

break;

elseif posit(l,:)==[s+1 t] %6

s= posit(l,1);t= posit(l,2);

posit(l,:)=[];

chain= [ chain 6];

break;

elseif posit(l,:)==[s+1 t+1] %7

s= posit(l,1);t= posit(l,2);

posit(l,:)=[];

chain= [ chain 7];

break;

end

end

end

disp(chain);

Αρχείο chaincode2

clear;

close all;

rgb = imread(‘example.bmp’);

A=gt_code(rgb);

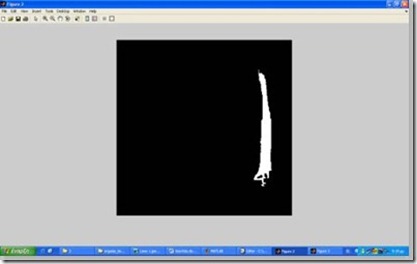
Η εικόνα πάνω στην οποία πραγματοποιείται η επίδειξη των αλγορίθμων είναι το αρχείο “example.png”. Στην αυθεντική της μορφή η εικόνα έχει ως εξής:

Στις οθόνες που ακολουθούν, επιστρέφεται διαδοχικά το αποτέλεσμα που προκύπτει από την εφαρμογή του αλγόριθμου chain code στο αρχικό αρχείο.

Για την υλοποίηση του αλγορίθμου differential chain code χρησιμοποιείται ένα σύνολο συναρτήσεων, οι οποίες είναι υλοποιημένες σε διαφορετικά αρχεία. Πιο συγκεκριμένα, υπολογιζεται πρωτα ο chain code και στη συνεχεια ο differential.

Αρχείο gt_code.m

 

function [CH_CODE] = gt_code(IM);

% This function generated the chain code from a binary image;

row = 1; col = 1;

[rr,cc] = size(IM);

% Scanning image to find the object

while IM(row,col) == 0,

if col == cc

row = row+1;col = 1;

else

col = col+1;

end

end

first_pt = [row,col]; % First point of the image

i = [0 1 1 1 0 -1 -1 -1];

j = [1 1 0 -1 -1 -1 0 1];

x = 0;

xm = mod(x,8)+1;

count = 0; % For stopping loop in case of just one pixal

%next_row = row + i(x); next_col = col + j(x);

while ( (IM(row+i(xm),col+j(xm)) == 0) & (count < 4) ), % Finding first element of chain code

x = x+1;

xm = mod(x,8)+1;

count = count + 1;

end

if count >= 4 % When image is just one point

CH_CODE = [];

DF_CODE = [];

else

CH_CODE = [x]; % First member of chain code

row = row + i(xm); col = col + j(xm);

% [row col]

x = x-2; %start checking for contour from this direction

xm = mod(x,8)+1;

count = 0;

while ( ((row ~= first_pt(1)) | (col ~= first_pt(2))) & (count < 8) ),

while ( (IM(row+i(xm),col+j(xm)) == 0) & (count < 8) ),

x = x+1; xm = mod(x,8)+1;

count = count+1;

end

CH_CODE = [CH_CODE x];

row = row + i(xm); col = col + j(xm);

% [row col]

x = x-2; xm = mod(x,8)+1;

count = 0;

end

end

Αρχείο gt_diff.m

 

function [x2,y] = gt_diff(IM);

% Get chain code of an image using get_code function

% Get differential chain code from the chain code

% The chain code is first resampled so that we get a constan size chain code.

x = gt_code(IM);

M = 128; % Length of difference code

N = length(x);

x2 = resample(x(1:N),M,N);

% x2 = round(x2);

% x2 = ((x2 <= 7) .* x2) + ((x2 > 7) .* 7);

% x2 = ((x2 >= 0) .* x2);

y(1) = x2(1) – x2(end);

nn = 2:length(x2);

y(nn) = x2(nn) – x2(nn-1);

y = mod(y+4,8)-4;

%y = x2;

Αλγόριθμος υπολογισμού κεντρικών και αναλλοίωτων ροπών και να γίνει επίδειξη της λειτουργίας του σε εικόνες.

Το σύνολο των ροών μιας φραγμένης συνάρτησης f(x,y) ορίζεται από τη σχέση:

,

όπου οι δείκτες j,k λαμβάνουν όλες τις μη αρνητικές ακέραιες τιμές. Το σύνολο όλων των ροπών 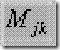, j,k={0,1,2,…..} προσδιορίζει πλήρως και μονοσήμαντα τη συνάρτησηf(x,y). Με τη βοήθεια των συντεταγμένων κέντρου βάρους, υπολογίζονται οι κεντρικές ροπές από την εξής σχέση:

όπου x’ , y’ οι συντεταγμένες του κέντρου βάρους και άκρα ολοκλήρωσης +∞ και -∞ . Στην συνάρτηση αυτή λοιπόν, περνάμε σαν παράμετρο μια εικόνα και τις τιμές των j,k .

Το βασικότερο πλεονέκτημα των κεντρικών ροπών είναι το γεγονός πως παραμένουν αναλλοίωτες σε μεταβολές της θέσης του αντικειμένου.

[παραπομπή]

Για την υλοποίηση ο αλγόριθμος υπολογισμού κεντρικού ροπών με τη βοήθεια του MATLAB, χρησιμοποιείται ένα σύνολο συναρτήσεων, οι οποίες είναι υλοποιημένες σε διαφορετικά αρχεία. Πιο συγκεκριμένα, ο κώδικας που χρησιμοποιείται για την υλοποίηση του αλγορίθμου υπολογισμού κεντρικών ροπών είναι ο εξής:

 

Αρχείο centralmoments.m

 

% gets a given central moment value

function muv = centralmoments (Image,u,v)

[r,c] = find(Image==1); % get (r,c) of region’s pixels

rbar = mean(r);

cbar = mean(c);

n = length(r);

momlist = zeros(n,1);

for i = 1 : n

momlist(i) = (r(i) – rbar)^u * (c(i) – cbar)^v;

end

muv = sum(momlist);